灵魂拷问：0.1 + 0.2 === 0.3 吗？

先说结果：在 JavaScript 中，0.1 + 0.2 是不等于 0.3 的。

解决方案

1. 使用 toFixed:

   jscopied
   parseFloat((0.1 + 0.2).toFixed(1)) === 0.3 // true
   

2. 转为整数运算：

   jscopied
   (0.1 * 10 + 0.2 * 10) / 10 === 0.3 // true
   

注意：这两种方案只针对 0.1 + 0.2，其它情况不一定适用。

为什么 0.1 + 0.2 !== 0.3？

在说为什么之前，我们需要了解一些前置知识。

前置知识

在 JavaScript 中，浮点数是基于 IEEE-754 中的**双精确度（64位）**标准进行存储的。也就是说，浮点数存储在内存空间中是一个64位的二进制小数的形式。

IEEE-754的64位双精度标准

• sign bit：符号位（1bit）0表示正数，1表示负数

• exponent：指数位（11bits），正数，0(特殊值，11位全是0)、2047（特殊值，11位全是1） 或 [-1022,1023] + 1023 转换成二进制的结果，不够11位则在前面补0

• mantissa：有效尾数（52bits），尾数中有一个隐藏位“1”。原因是在二进制中，第一个有效数字必定是“1”，为了能够存储多一位精度，这个“1”并不会存储。

科学计数法

当我们要标记或运算某个较大或较小且位数较多时，用科学计数法免去浪费很多的空间和时间。

比如：1000000000使用科学计数法表示为：1 * 10 ^ 9；0.001使用科学计数法表示为：1 * 10 ^-3；0.1使用科学计数法表示为：1 * 10^-1。

指数位计算

0.1在科学计数法中，指数位为-4，所以 exponent 中存储是值是：-4 + 1023 = 1019 ,转换成二进制为：1111111011 ,不足11位，则在前面补0：01111111011

有效数计算过程

0.1存储的值：

在计算机中，有效数转换成二进制是通过乘以2(*2)，如果结果大于1，则取乘积的小数部分继续乘以2，结果为0终止计算，最终结果是取每一次乘积中的整数位：

plain-textcopied
0.1 转换成二进制过程

0.1 * 2 = 0.2
0.2 * 2 = 0.4
0.4 * 2 = 0.8
0.8 * 2 = 1.6
0.6 * 2 = 1.2
0.2 * 2 = 0.4
0.4 * 2 = 0.8
0.8 * 2 = 1.6
0.6 * 2 = 1.2
0.2 * 2 = 0.4
0.4 * 2 = 0.8
0.8 * 2 = 1.6
0.6 * 2 = 1.2
0.2 * 2 = 0.4
0.4 * 2 = 0.8
0.8 * 2 = 1.6
0.6 * 2 = 1.2
...

可以看出，后面是一段重复的运算过程，最后得出来的结果是：

plain-textcopied
00011001100110011001100110011001100110011001100110011...

也就是：

plain-textcopied
0.00011001100110011001100110011001100110011001100110011... * 2^0

因为浮点数的存储首位必须是1，也就是1.bbbbb.... * 2^n 这种形式，所以我们需要将这个结果进行转换：

plain-textcopied
0.1
=> 0.00011111111100001100110011001100110011001100110011001100110011001...
=> 0.0001100110011001100110011001100110011001100110011001... * 2^0
=> 1.100110011001100110011001100110011001100110011001... * 2^-4

而且有效数只能是52位，所以我们需要对结果进行截取，在十进制中我们有四舍五入的说法，而在二进制中是零舍一入：

plain-textcopied
1.1001100110011001100110011001100110011001100110011001|1001

我们可以看到从小数点后面算第53位是1，需要向前进位：

plain-textcopied
1.1001100110011001100110011001100110011001100110011010

并且小数点前面的 “1” 在存储时，会被隐藏，所以最终存储的52有效数是：

plain-textcopied
1001100110011001100110011001100110011001100110011010

从上面的分析，可以得出 0.1 存储的值为：

plain-textcopied
0|01111111011|1001100110011001100110011001100110011001100110011010
// 去掉分隔线后
0011111110111001100110011001100110011001100110011001100110011010

因为存在一个截取过程，所以 0.1在计算机中存储的值是和我们认知中的 0.1不相等的。

0.2存储的值：

有效数计算：

plain-textcopied
0.2 * 2 = 0.4
0.4 * 2 = 0.8
0.8 * 2 = 1.6
0.6 * 2 = 1.2
0.2 * 2 = 0.4
0.4 * 2 = 0.8
0.8 * 2 = 1.6
0.6 * 2 = 1.2
0.2 * 2 = 0.4
0.4 * 2 = 0.8
0.8 * 2 = 1.6
0.6 * 2 = 1.2
0.2 * 2 = 0.4
0.4 * 2 = 0.8
0.8 * 2 = 1.6
0.6 * 2 = 1.2
...

有效数结果为:

plain-textcopied
00110011001100110011001100110011001100110011001100110011

也就是：

plain-textcopied
0.00110011001100110011001100110011001100110011001100110011 * 2^0
=> 1.1001... * 2^-3

可以得出 0.2 的存储值为：

plain-textcopied
0|01111111100|1001100110011001100110011001100110011001100110011001|1001
// 截取且去掉分隔线后
0011111111001001100110011001100110011001100110011001100110011010

二进制四则运算规则

步骤：

1. 对阶，使得两个数的小数位对齐；
2. 尾数求和，将两个数对阶之后按照定点的加减法运算规则计算；
3. 规格化，为了增加有效数的位数，必须将求和（差）之后的尾数进行规格化；
4. 舍入，64位存储中的有效数只能存储到52位，所以需要对53位之后的数值进入舍入（默认：0舍1入）；
5. 溢出判断，判断计算结果是否存在溢出。

0.1 + 0.2 的计算过程

对阶

我们先看看科学计数法的运算规律：

plain-textcopied
100 + 1000 = 1100
100 + 1000
= 1 * 10^2 + 1 * 10^3
= 0.1 * 10^3 + 1 * 10^3
= (0.1 + 1) * 10^3
= 1.1 * 10^3

-----
12300 + 45600 = 57900
12300 + 45600
= 1.23 * 10^4 + 4.56 * 10^4
= (1.23 + 4.56) * 10^4
= 5.79 * 10^4

从上面的分析可以看出，科学计数法的计算时，可以先转换成最大阶码形式，提取公因式之后再进行运算。

所以我们在计算的时候，先要执行对阶操作，为了保证更好的精确度，我们采用的是小阶对大阶的形式来完成对阶

plain-textcopied
0.1 => 0|01111111011|1001100110011001100110011001100110011001100110011010
0.2 => 0|01111111100|1001100110011001100110011001100110011001100110011010

阶差：

plain-textcopied
 01111111100
-01111111011
------------
=00000000001

0.2 的阶码比 0.1 的阶码大，阶差为 01111111100 - 01111111011 , 结果是 1，所以 0.1 需要升一阶。

升阶的形式是尾数右移，每右移一位，阶码 + 1。

注意：右移升阶时，会把隐藏位的 1 给挤出来

plain-textcopied
0.1 => (1).100110011001100110011001100110011001100110011001100110 * 2^01111111011
    => (0).1100110011001100110011001100110011001100110011001100110 * 2^01111111100

尾数运算

plain-textcopied
  (0).11001100110011001100110011001100110011001100110011010
 +(1).1001100110011001100110011001100110011001100110011010
----------------------------------------------------------
=(10).01100110011001100110011001100110011001100110011001110 * 2^01111111100

规格化

有效数的第一位的取值只能是 1，需要对结果进行规格化，

plain-textcopied
(10).01100110011001100110011001100110011001100110011001110 * 2^01111111100
=> (1).001100110011001100110011001100110011001100110011001110 * 2^01111111101

有效数截取

遵循零舍一入的原则：

plain-textcopied
(1).001100110011001100110011001100110011001100110011|001110 * 2^01111111101
=> (1).001100110011001100110011001100110011001100110011|001110* 2^01111111101

溢出判断

指数位为 01111111101，并没溢出。

0.1 + 0.2 的结果

所以 0.1 + 0.2 的结果为：

plain-textcopied
0|01111111101|0011001100110011001100110011001100110011001100110011
// 移除分隔线
0011111111010011001100110011001100110011001100110011001100110011

转为十进制：

plain-textcopied
(1).0011001100110011001100110011001100110011001100110011 * 2^01111111101
// 降阶
=>(0).010011001100110011001100110011001100110011001100110011 * 2^0
// 截取
=>0.0100110011001100110011001100110011001100110011001101 * 2^0
// 转为 10 进制
=> 0.30000000000000004

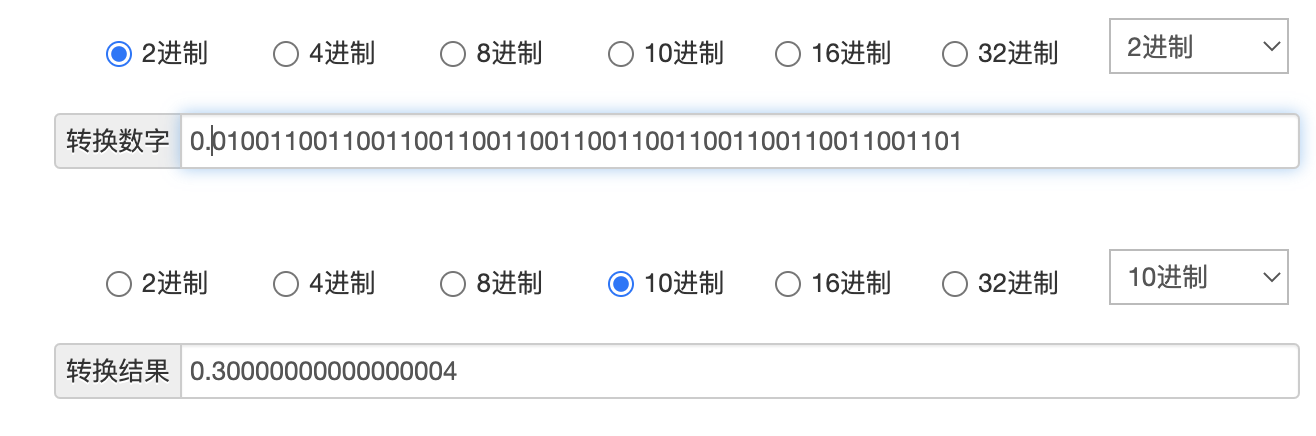
浏览器控制台计算 0.1 + 0.2 的结果如下：

可以看出我们的计算是没有什么问题的，这也印证了为什么 0.1 + 0.2 不等于 0.3。

为什么 0.1 + 0.3 === 0.4

0.1 + 0.2 我们都学会了怎么计算了，0.1 + 0.3 那不是信手拈来？

我们在上面已经计算出了 0.1 和 0.3 的小数位表示方式：

plain-textcopied
0.1 => 0|01111111011|1001100110011001100110011001100110011001100110011010
0.3 => 0|01111111101|0011001100110011001100110011001100110011001100110011

对阶：

阶差为2，且 0.1是小阶：

plain-textcopied
0.1 => 0|01111111011|1001100110011001100110011001100110011001100110011010
    => 1.1001100110011001100110011001100110011001100110011010 * 2^01111111011
    => 0.011001100110011001100110011001100110011001100110011010 * 2^01111111101

有效数计算

plain-textcopied
 0.011001100110011001100110011001100110011001100110011010 * 2^01111111101
+1.0011001100110011001100110011001100110011001100110011 * 2^01111111101
---------------------------------------------------------------------------
=1.1001100110011001100110011001100110011001100110011001|10 * 2^01111111101

规格化

小数点右边是1，已经是规格数。

有效数截取：

plain-textcopied
1.1001100110011001100110011001100110011001100110011010 * 2^01111111101

溢出判断：

指数 01111111101 无溢出。

01 + 0.3 的结果:

plain-textcopied
0|01111111101|1001100110011001100110011001100110011001100110011010
// 移出分隔线
0011111111011001100110011001100110011001100110011001100110011010

转为十进制：

plain-textcopied
1.1001100110011001100110011001100110011001100110011010 * 2^01111111101
=> 0.011001100110011001100110011001100110011001100110011010 * 2^0
=> 0.4 * 10^1

所以，0.1 + 0.3 是等于 0.4 的

为什么说 toFixed 不安全？

我们先看看 toFixed 的一些结果：

通过上图，我们可以看出，toFixed 的截取有点诡异。

我们认知中的四舍五入的原则，运算结果应该是这样的：

jscopied
0.445.toFixed(2) // 0.45
0.446.toFixed(2) // 0.45
0.435.toFixed(2) // 0.44
0.4356.toFixed(2) // 0.44

我们再看看下面的例子：

再来个对比：

为什么会造成这么诡异的情况呢？这是一种叫四舍六入五成双的进位方法：对于位数很多的近似数，当有效位确定后，其后面多余的数字应该舍去，只保留有效数最后一位，这种舍入规则是“四舍六入五成双”。

这种规则也叫“四舍六入五凑偶”：

• 四舍：指小于或等于4时，直接舍去；
• 六入：指大于或等于6时，舍去后进1；
• 五凑偶：当5后面还有数字时，舍5进1；当5后面没有数字或为0时，需要分为以下几种情况：
  • 5前面的数字小于等于4时：偶数则舍5进1；奇数直接舍去；
  • 5前端的数字大于4时：舍5进1。

所以说，我们使用 toFixed 的方案来解决浮点数的运算问题，是不安全的。

为什么乘以高倍数后再运算不安全？

我们先看一下十进制下乘法运算是怎么做的

plain-textcopied
0.1 * 0.2

  0.1
* 0.2
------
= 0.02


1.12 * 2.2

  1.12
* 2.20
------
     0
  224
 224
------
2.4640

也可以这样子
  1.12
*  2.20
------
=2.4640

Q：16.1 * 1000 === 16100？

plain-textcopied
16.1 => 10000.0001100110011001100110011001100110011001100110011001...
     => 1.0000000110011001100110011001100110011001100110011010 * 2^10000000011

1000 => 1111101000.000000...
     => 1.1111010000000000000000000000000000000000000000000000 * 2^10000001000

阶码相加：

plain-textcopied
 10000000011
+10000001000
------------
=100000001011

2059 - 1023 = 1036 = 10000001100

尾数相乘：

plain-textcopied
           1.000000011001100110011001100110011001100110011001101|0
                                                        1.111101|00000000000...
-----------------------------------------------------------------------------
      0000001000000011001100110011001100110011001100110011001101
      0000000000000000000000000000000000000000000000000000000000
      00001000000011001100110011001100110011001100110011001101
      0001000000011001100110011001100110011001100110011001101
      001000000011001100110011001100110011001100110011001101
      01000000011001100110011001100110011001100110011001101
      1000000011001100110011001100110011001100110011001101
-----------------------------------------------------------------------------
===>
 0000001000000011001100110011001100110011001100110011001101
 0000000000000000000000000000000000000000000000000000000000
+0000100000001100110011001100110011001100110011001100110100
-----------------------------------------------------------
=0000101000010000000000000000000000000000000000000000000001

+0001000000011001100110011001100110011001100110011001101000
+0010000000110011001100110011001100110011001100110011010000
-----------------------------------------------------------
=0011000001001100110011001100110011001100110011001100111000

+0100000001100110011001100110011001100110011001100110100000
+1000000011001100110011001100110011001100110011001101000000
-----------------------------------------------------------
=1100000100110011001100110011001100110011001100110011100000
-----------------------------------------------------------------------------
===>
 0000101000010000000000000000000000000000000000000000000001
+0011000001001100110011001100110011001100110011001100111000
-----------------------------------------------------------
=0011101001011100110011001100110011001100110011001100111001

+1100000100110011001100110011001100110011001100110011100000
-----------------------------------------------------------------------------
===>
 0011101001011100110011001100110011001100110011001100111001
+1100000100110011001100110011001100110011001100110011100000
-----------------------------------------------------------
=1111101110010000000000000000000000000000000000000000011001

最终运算出来的结果是
1.111101110010000000000000000000000000000000000000000011001 * 2^10000001100
截取之后等于
1.1111011100100000000000000000000000000000000000000001 * 2^10000001100
换算成十进制
11111011100100.000000000000000000000000000000000000001 * 2^0
=16100.000000000002

通过上面的运算，我们发现乘以一个更大的倍数后再计算也是不安全的。

最终解决方案

所以需要比较精确的浮点数运算，我还是建议使用一些现有的库来完成计算。例如：decimal.js

jscopied
import Decimal from 'decimal.js'

const a = new Decimal(0.1)
const b = a.add(0.2)

console.log(b.toNumber()) // 0.3

const c = new Decimal(16.1)
const d = c.mul(1000)

console.log(d.toNumber()) // 16100

附

Node中浮点数转二进制字符方法

jscopied
/**
 * floatToBinStr
 * 浮点数转成二进制字符
 * @param {number} input
 */

function floatToBinStr (input) {
  if (typeof input !== 'number') {
    throw new TypeError('parameter `input` must be a number type.')
  }

  const buff = Buffer.allocUnsafe(8)
  buff.writeDoubleBE(input)

  let binStr = ''

  for (let i = 0; i < 8; i++) {
    binStr += buff[i].toString(2).padStart(8, '0')
  }

  return {
    output: binStr,
    // 符号 0 => 正；1 => 负
    sign: binStr[0],
    // 指数
    exponent: binStr.slice(1, 12),
    // 有效尾数
    mantissa: binStr.slice(12),
    // 科学计数法
    scientificNotation: `(-1)^${binStr[0]}*1.${binStr.slice(12)}*2^${Number(`0b${binStr.slice(1, 12)}`) - 1023}`
  }
}

[0.1, 0.2, 0.3, 0.4, 16.1, 1000.0].forEach(number => {
  console.log(`----- ${number} ---------------`)
  const { output, sign, exponent, mantissa, scientificNotation } = floatToBinStr(number)
  console.log(`输出: ${output}`)
  console.log(`符号: ${sign}`)
  console.log(`指数: ${exponent}`)
  console.log(`有效尾数: ${mantissa}`)
  console.log(`科学计数法: ${scientificNotation}`)
  console.log('-------------------------------')
})

浮点数调用 toString(2) 为什么返回的结果长度不一样？

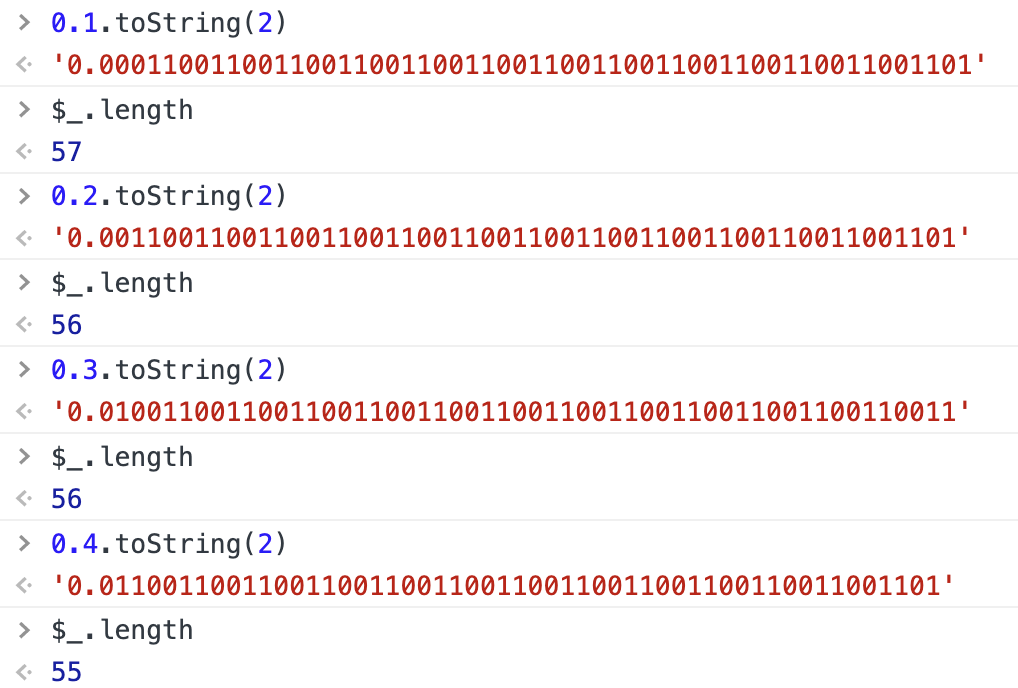
为什么呢？

我们先看下这几个数存储的内容是什么：

plain-textcopied
0.1 => 0|01111111011|1001100110011001100110011001100110011001100110011010
0.2 => 0|01111111100|1001100110011001100110011001100110011001100110011010
0.3 => 0|01111111101|0011001100110011001100110011001100110011001100110011
0.4 => 0|01111111101|1001100110011001100110011001100110011001100110011010

JS在转成字符串时，会将阶数变成 0，转换完成后会舍弃后面为0的位，然后再输出：

plain-textcopied
0.1 => 1.1001100110011001100110011001100110011001100110011010 * 2^01111111011
    => 0.00011001100110011001100110011001100110011001100110011010 * 2^0
    => '0.00011001100110011001100110011001100110011001100110011010'
    // 舍弃后面无用的0
    => '0.0001100110011001100110011001100110011001100110011001101'
length: 57
		
0.2 => 1.1001100110011001100110011001100110011001100110011010 * 2^01111111100
    => 0.0011001100110011001100110011001100110011001100110011010 * 2^0
    => '0.0011001100110011001100110011001100110011001100110011010'
    // 舍弃后面无用的0
    => '0.001100110011001100110011001100110011001100110011001101'
length: 56
		
0.3 => 1.0011001100110011001100110011001100110011001100110011 * 2^01111111101
    => 0.010011001100110011001100110011001100110011001100110011 * 2^0
    => '0.010011001100110011001100110011001100110011001100110011'
length: 56
		
0.4 => 1.1001100110011001100110011001100110011001100110011010 * 2^01111111101
    => 0.011001100110011001100110011001100110011001100110011010 * 2^0
    => '0.011001100110011001100110011001100110011001100110011010'
    // 舍弃后面无用的0
    => '0.01100110011001100110011001100110011001100110011001101'
length: 55